Covid-19 : le début de la fin ? (1)

Tout au long du mois de mai, les analyses des eaux usées de l’usine d’épuration de Cape Canaveral en Floride n’ont détecté aucune présence du nouveau coronavirus, du moins jusqu’à la semaine du 27 mai : avec le lancement historique des astronautes américains Bob Behnken et Doug Hurley vers l’ISS, tout le monde a convergé vers le Cape et les tests de cette semaine-là ont révélé une concentration du virus correspondant à au moins 85 malades du Covid-19.

Quatre semaines plus tard, entre le 29 juin et le 12 juillet, les morts du Covid-19 en Floride étaient beaucoup plus jeunes qu’auparavant, plus de 20 % ayant moins de 65 ans.

Début juin, selon ABC News, l’épidémie semblait avoir repris un peu partout et les experts américains avertissaient d’une possible seconde vague. Au Texas, le gouverneur était obligé de restaurer l’obligation de porter un masque pendant que son homologue de Louisiane avertissaitque « les progrès contre le coronavirus ont été anéantis au cours des trois dernières semaines »alors que les soins intensifs opéraient à pleine capacité dans certains établissements hospitaliers. Non seulement les cas et les hospitalisations augmentaient (jusqu’à 97 % à Orange County, un des plus grands comtés de Californie) mais les décès remontaient également.

Plus près de nous, Israël, qui a eu une gestion relativement meilleure de la crise, refermait ses bars, ses boîtes de nuit et ses salles de sport. Le Maroc plaçait en quarantaine la ville de Safi et ses 300 000 habitants, les soumettant à un confinement total.

En Espagne, qui a suivi la crise de façon aussi désordonnée et catastrophique que la France, le gouvernement « se retrouve maintenant avec des nouveaux foyers qui l’obligent à repasser à des confinements qui, cette fois-ci, sont localisés » explique Arnaud Fontanet, épidémiologiste à l’Institut Pasteur, et membre du Conseil scientifique sur le coronavirus, ajoutant que la situation en Espagne « est vraiment un signal d’alerte pour nous ».

Avons-nous affaire à une seconde vague ? Ou est-ce le début de la fin ? Rien n’est parfaitement certain et dépend de deux facteurs, le degré de contagion R0 et la sérologie effective.

ÉPIDÉMIOLOGIE DE BASE

En épidémiologie, le nombre de reproduction de base ou R0 d’une infection est le nombre moyen de nouveaux cas générés par chaque malade dans une population où tous les individus sont susceptibles et avant que ne soient prises des mesures prophylactiques particulières :

• moyen car certains individus n’infectent personne et que d’autres sont les précurseurs à de multiples chaînes d’infection ;
• une population susceptible car R0 n’a de sens qu’au début d’une épidémie quand tous les individus sont sains sauf un ;
• et avant que les comportements ne changent, soit volontairement, soit par diktat étatique, c’est-à-dire au début d’une épidémie.

Pour Covid-19, 80 % des nouvelles transmissions seraient causées par moins de 20 % des porteurs selon un récent article (preprint) sur la transmission à Hong Kong. La grande majorité des malades n’en infectent de nouveaux que très peu ou pas du tout. Seule une minorité sélective d’individus, les sur-propagateurs (super-spreaders en anglais) propagent le virus de manière agressive comme dans le cas des églises de Corée du Sud ou de celle de l’État de Washington.

Le R0 n’est donc pas un nombre réel : c’est en fait une variable aléatoire dont on exprime en général la moyenne, pour faire simple : en fait, les épidémiologistes ont aussi une mesure de sa dispersion (une sorte d’inverse de sa variance), k, qui est d’autant plus faible que la maladie a de nombreux clusters. Lorsque la maladie n’a pas de clusters, k est proche de 1 comme pour la grippe saisonnière.

En 2005, dans un article fondamental de Nature, Lloyd-Smith et ses co-auteurs ont estimé que le SARS-CoV (de 2003) – dans lequel la sur-propagation jouait un rôle majeur – avait un k de 0,16. Le k estimé pour le MERS, apparu en 2012, serait d’environ 0,25. Pour SARS-CoV-2, les estimations de k varient selon les sources de 0,20 à 0,10 avec un intervalle de confiance à 95 % (IC à 95 %) de 0,20 à 0,04 dans ce dernier cas.

Si k est vraiment inférieur ou égal à 0,10, la plupart des infections ne donnent pas lieu à d’autres infections. Par contre, dans quelques cas, un malade en infecte des dizaines d’autres.

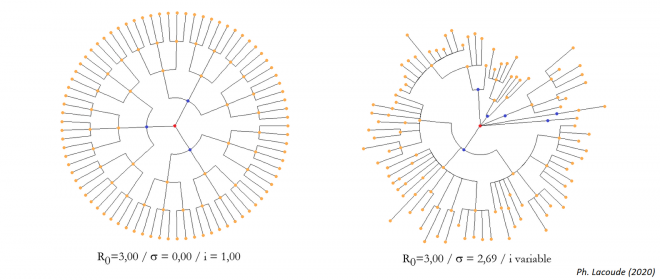
Pour illustrer le problème, considérons deux arbres phylogénétiques (que j’ai réalisés avec R). Dans les deux, j’ai fixé la transmission à R0=3,0 en partant du patient zéro en rouge.

Dans le premier, à gauche, j’ai considéré qu’il n’y avait pas de variance (écart-type nul), le patient zéro infecte trois personnes (en bleu) qui chacune en infectent à leur tour 3, etc. 1, 3, 9, 27, 81… La période d’incubation est fixée à une unité de temps.

Dans le second cas, à droite, j’ai introduit un écart-type non nul. Le R0 est toujours de trois mais les patients infectent trois personnes en moyenne avec une variance non-nulle. La période d’incubation est également variable mais de même moyenne.

Clairement, dans les deux cas, le R0 de la maladie est de 3,0 mais dans le second cas, la distribution de la variable aléatoire que représente en fait R0 est différente. De nombreux patients ne transmettent la maladie qu’une seule fois. D’autres la transmettent plus de dix fois : au final, c’est le même taux (moyen) de contagion.

Sauf que nous comprenons bien que si la maladie se comporte comme dans le graphique de gauche, elle ne peut pas être dormante pendant longtemps. En fait, elle ne peut pas être dormante !

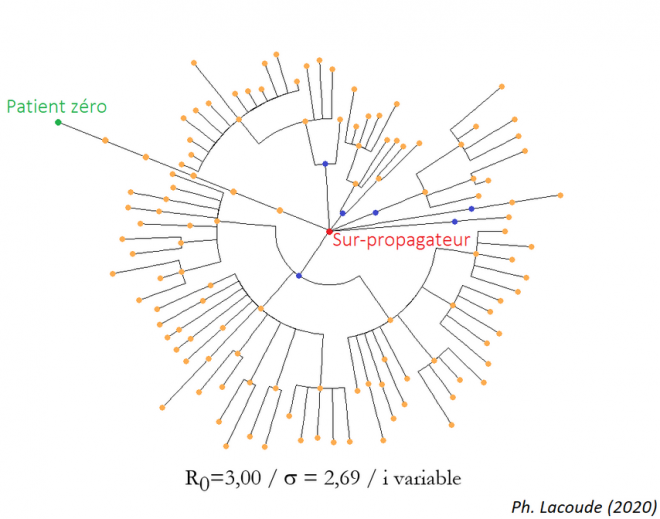
Au contraire, si le k du SARS-CoV-2 est proche de 0,10 c’est-à-dire si la maladie se comporte plutôt comme dans l’arbre phylogénétique de droite, il existe la possibilité que la chaîne partie du patient zéro de Wuhan n’ait été qu’une longue branche mince de sous-propagateurs avant qu’elle ne rencontre finalement un sur-propagateur qui a finalement fait exploser le Covid-19 en pandémie mondiale :

Dans l’exemple ci-dessus, le patient zéro (vert) n’infecte qu’une seule autre personne qui n’en infecte qu’une à son tour, etc. jusqu’à ce qu’on atteigne un sur-propagateur (en bleu). Au lieu d’avoir {1, 6, 7, 26, 81, 243,…} malades à chaque génération, nous avons {1, 1, 1, 1, 1, 1, 6, 7, 26, 81, 243,…} malades. Ça ne change (presque) rien au R0 ou à la variance empiriques car ce sont les grosses générations futures qui « comptent ».

Par contre, ceci change tout à l’histoire de la pandémie car dans le cas de Covid-19, les malades mettent en moyenne 5,2 jours à incuber et sont malades pendant 14 jours (en moyenne !). Une « génération » de malades est donc de 5,2+7 jours : le début de notre série {1, 1, 1, 1, 1, 1, 6} s’écoule donc (en moyenne) sur 73 jours au lieu de 12 jours dans l’exemple {1, 6} précédent !

Si le coefficient k est exceptionnellement bas, il est possible (mais peu probable) d’avoir de telles chaines phylogénétiques : une maladie dormante pendant des semaines où chaque patient ne transmet qu’à un ou deux autres patients. L’arbre phylogénétique sans branche ou avec des toutes petites branches qui n’ont pas de feuilles. Ou presque…

En revanche, dès que l’on commence à avoir des cas en nombre, c’est-à-dire des branches à cet arbre, la probabilité que chacune d’entre elles meure devient proche de zéro. Ceci laisse une marge de manœuvre pour quelques cas en dehors de la Chine, par exemple, un cas à Paris, deux au Brésil, un à Milan, etc. entre le patient zéro et le 31 décembre 2019. Chacune de ces chaines est morte ou a végété.

Mais les branches qui sont dans les pays dont je viens de faire mention ne peuvent pas avoir eu plus de quelques cas sinon c’est l’exponentielle de Wuhan en janvier, de Milan en février, de Paris en mars, de New York City en avril…

Quoi qu’il en soit, tout arbre phylogénétique hypothétique doit réconcilier les données cliniques et génétiques dont nous disposons. Cependant, il est évident qu’une simple simulation par la méthode de Monte Carlo ferait apparaître de multiples scénarios – peu plausibles mais pas impossibles – où, sans changer ni R0 ni k, le SARS-CoV-2 passe de l’animal à l’Homme des mois avant que n’apparaissent une cinquantaine de cas à Wuhan à la fin décembre 2019.

Ce qu’il est important de retenir, c’est que plus k est bas, c’est-à-dire que la variable aléatoire R0est variante, et moins les scénarios peu plausibles le sont vraiment.

Les récents calculs de la variance de la transmission de SARS-CoV-2 – qui apparaît comme très élevée – expliqueraient donc de nombreuses données bizarres de la maladie Covid-19 :

• Tout d’abord, il aurait fallu que le virus soit exporté en moyenne au moins 4 fois d’un pays X à un pays Y pour que l’épidémie démarre dans le pays Y. Ceci expliquerait la lenteur de la propagation initiale de la maladie d’une région à une autre.

• Ceci renforce les effets de clusters : la géographie a une part prépondérante (ici). Comme l’ont montré mes anciens collègues du Center for Data Analysis, le Covid-19 à New York et dans le New Jersey s’est presque entièrement concentré autour du dense réseau de trains de banlieue qui mènent à Manhattan. Ceci implique que les politiques de confinement indifférenciées sont ineffectives (ici et là).

• Ceci confirmerait les données génétiques (que nous citions dans un billet début février) qui permettent, en utilisant les caractéristiques liées à l’horloge moléculaire telles que le taux de substitution des nucléotides, de déduire qu’il y a 90 % de probabilité que SARS-CoV-2 soit apparu entre le 27 juin et le 29 octobre 2019, soit 3 à 6 mois environ, avant l’épidémie. Bien sûr, ceci laisse 5% de probabilité qu’il soit apparu avant et 5 % de probabilité qu’il soit apparu après.

• Ceci donnerait une infime chance à la possibilité que les traces de SARS-CoV-2 aient vraiment été trouvées dans un échantillon des eaux usées de Santa Catalina, au Brésil, en novembre 2019 !

• Dans le même ordre d’idée, que j’accepterais aussi avec une extrême prudence, SARS-CoV-2 aurait pu être présent dans les eaux usées de Barcelone le 12 mars 2019 ! Si ce n’est pas une erreur de manipulation ou un faux positif (peu probable mais possible) des tests PCR, un habitant de Wuhan, malade, aurait bel et bien visité la capitale catalane. Ceci me semble très peu probable mais, compte-tenu du très faible k de SARS-CoV-2, pas complètement impossible.

Si ces deux derniers résultats sont corrects et, a fortiori, si nous en découvrons de nouveaux, de très nombreuses branches des chaînes d’infection disparaissent d’elles-mêmes. Et il y a donc (nécessairement) beaucoup plus de sur-propagateurs que nous ne le pensons !

LES MODÈLES SIR ET SEIR

Les épidémiologistes classent une population donnée en « compartiments » : à chaque temps t, il a des gens sains susceptibles S(t), des patients infectés I(t), et des gens qui s’en sont remis R(t). Parfois, on considère les patients exposés E(t) qui sont en période d’incubation. Pour certaines maladies, on a besoin d’autres compartiments que je passerai ici sous silence.

Les modèles s’appellent donc SIR ou SEIR, selon leurs compartiments.

Les gens passent d’un compartiment à l’autre. À chaque instant t, des gens susceptibles S(t) sont exposés E(t) puis deviennent infectés I(t) et s’en remettent R(t) ou décèdent (si on a un compartiment D(t) pour les décès). La population I(t) ne peut pas infecter les gens qui s’en sont remis R(t) (ni bien sûr ceux qui sont décédés).

Sans mystère, la somme S(t)+E(t)+I(t)+R(t) (plus, éventuellement, D(t) pour les décès) est égale à la population N de départ qu’on peut prendre comme constante pour COVID-19.

Au départ, I(0) = 1 qui est le patient zéro et S(0) = N – 1.

La dérivée de S’(t) en fonction du temps vaut -β.I(t).S(t)/N où β est une moyenne de contacts producteurs d’infection par unité de temps. Comme β, I(t) et S(t) sont positifs, le nombre de personnes susceptibles décroît.

La dérivée des infections I’(t) est évidemment égale aux nouveaux malades S’(t) moins ceux qui guérissent en proportion γ (qui est aussi l’inverse de la période moyenne d’infection). Du coup, I’(t) = β.I(t).S(t)/N – γ.I(t).

En français, les nouvelles infections sont égales à une constante β multipliée par le nombre de malades I(t) multiplié par la proportion de personnes saines qui est S(t)/N moins le nombre de personnes qui guérissent qui est évidemment γ% de ceux qui sont malades I(t).

Bien sûr, la dérivée de ceux qui guérissent R’(t) est égale à γ.I(t), c’est-à-dire la partie des infectés qui guérissent à chaque période de temps.

Les gens passent d’un compartiment à l’autre sans disparaitre : la somme des changements est égale à zéro. Si j’ai +n personnes dans un compartiment, j’ai -n personnes dans les autres. La somme des dérivées de ces fonctions est donc égale à 0 !

Ces équations différentielles ordinaires (EDO) sont extrêmement communes et se rencontrent dans tous les modèles démographiques, dans les modèles actuariels d’assurance-vie, en économie, en chimie, en économétrie, en médecine et dans certains réseaux de neurones artificiels.

Quel est le nombre attendu de nouvelles infections dans une population où tous les sujets sont sensibles sauf un, le patient zéro ? C’est évidemment R0 par sa définition même !

Mais comme β est la moyenne de contacts producteurs d’infection par unité de temps et que 1/γ est aussi la période moyenne d’infection, R0 = β/γ !

Sans résoudre aucune équation ! Voilà ! Nous sommes tous spécialistes du R0 comme le reste des utilisateurs de Facebook !

LE R0 EST PRIMORDIAL

Le ratio R0 est primordial : simple et complètement intuitif – à combien de personnes vais-je passer une maladie contagieuse ? –, il apparaît donc naturellement dans les mathématiques des modèles épidémiologiques.

Si le R0 est inférieur à 1,0 alors la dérivée I’(t) ci-dessus est négative et la grandeur I(t) le nombre de personnes infectées est décroissante : l’épidémie s’arrête !

A contrario, si le R0 est supérieur à 1,0 alors l’épidémie ne s’arrête que lorsque 1-1/R0 pourcent de la population a été infectée ou immunisée. Ceci est une simple conséquence des équations différentielles qui régissent la dynamique de l’épidémie.

Le R0 en détermine l’issue : si personne n’est immunisé et si je passe mon virus à trois personnes en moyenne (i.e. si R0 = 3,0) au cours de ma convalescence, je vais infecter trois nouveaux malades. A contrario, dès que deux-tiers des gens que je rencontre sont immunisés, je ne vais en infecter qu’une seule puisque les deux autres seront immunisées.

Ainsi, si R0 est 2,0, alors l’épidémie prend fin lorsque 50 % de la population a été infectée et s’en est remise. Si R0 est de 3,0, alors près de 67 % de la population doit avoir été infectée avant que les choses ne redeviennent normales. Si le R0 est de 4,0, alors près de 75 % de la population va être infectée.

Encore une fois, les processus en jeu sont aléatoires et l’infection se développe en clusters(comme on peut le voir sur ces simulations fascinantes).

Lorsque la pandémie de grippe H1N1 2009 a commencé, son R0 était estimé entre 1,2 et 1,6 ce qui impliquait que 16,7 % à 37,5 % de la population finisse infectée. Aux États-Unis, il y a 325 millions d’habitants et 16,7 % à 37,5 % représente donc 54 à 122 millions de personnes. Au final, 61 millions d’Américains ont été infectés selon le CDC.

LE NOMBRE DE REPRODUCTION DE BASE DE SARS-COV-2

Pour le SRAS-CoV-2, les estimations actuelles du R0 dans la littérature scientifique varient de 0,91 (en Lituanie, fin mars) à 7,4 (en Turquie en avril).

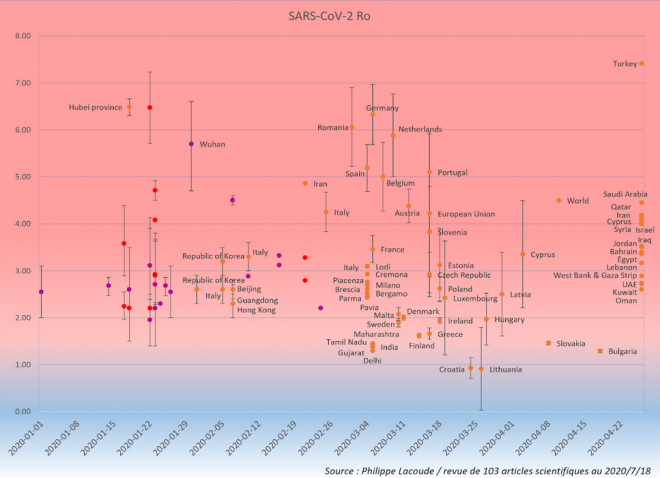
En cherchant tous les articles scientifiques sur le sujet, environ 120 depuis le début de la crise, il est possible de retenir 95 estimations fondées sur des études solides (par exemple ici, là ou là). Pour les résumer, on peut se référer à la période que recouvrent les données de chaque étude et examiner les résultats pour les différentes régions (avec la Chine en rouge et Wuhan en violet) :

Comme on peut le voir, la vaste majorité des études trouvent un R0 d’environ 3,0 pour le SARS-CoV-2. Il y a cependant quelques exceptions notables : soit des valeurs basses dans des zones rurales, soit des valeurs hautes que l’on peut attribuer à de mauvaises habitudes (politiques ou sanitaires).

Certains pays comme la Croatie, la Lituanie, la Slovaquie, ou la Bulgarie ont clairement bénéficié de l’expérience de leurs voisins : en fait, la population avait déjà changé ses habitudes lorsque SARS-CoV-2 est apparu et le R0 calculé à l’aide des premières données est très bas.

Notablement, c’est aussi le cas en Inde où le R0 est très bas (même si des doutes persistent quant aux données). Si en pratique, c’est excellent car ceci veut dire que la maladie y est moins contagieuse, en théorie, ce n’est pas une bonne chose : le R0 est le taux de reproduction de base, c’est-à-dire celui qui prévaudrait naturellement sans changements comportementaux.

Les études faites en utilisant des données au début de l’épidémie dans une région donnée sont donc plus fiables que celles qui utiliseraient des données après que l’épidémie ait commencé à changer les habitudes.

Comme l’explique un fascinant article d’Harvard Magazine, ces mesures basses d’avril et mai cachent potentiellement une réalité moins rose : l’épidémiologiste Marc Lipsitch, professeur au Harvard T.H. Chan School of Public Health souligne que « l’opinion selon laquelle [le R0] est aussi élevé [que 5,7 …] semble toujours être une opinion minoritaire, mais je pense que c’est une opinion crédible » même s’il ajoute prudemment qu’il n’a pas encore décidé « dans quelle mesure jauger [la] possibilité » que le nombre atteigne 5 ou 6.

Enfin, il est notable qu’il existe de nombreuses méthodes empiriques de calcul du R0. Ces 96 estimations sont issues d’une demi-douzaine de ces méthodes. En fait, même avec les mêmes données appliquées au même modèle SIR ci-dessus, il est possible d’obtenir de petites différences de quelques dixièmes de point. En pratique, chaque résultat devrait être interprété en fonction de la théorie sous-jacente.

Ceci étant précisé, il y a peu de chances que toutes ces études soient simultanément fausses :

• tout d’abord, les épidémiologistes ne sont pas tous systématiquement incompétents ;
• il y a longtemps que l’on aurait découvert que les modèles SIR ou SEIR sont mauvais ;
• les mathématiques qu’ils contiennent sont très bien comprises et utilisées dans de très nombreux domaines des sciences physiques, biologiques et humaines ;
• enfin, les modèles SIR et SEIR fonctionnent très bien pour toutes les autres épidémies.

QUE NOUS DISENT CES ÉTUDES ?

Même si le R0 n’est pas la seule mesure importante de l’épidémie, il nous faut donc accepter l’idée qu’il y a du vrai dans ces résultats.

Paradoxalement d’autant plus que la plage des estimations est importante, il y a peu de chance que le « vrai » R0 n’ait pas été « deviné » correctement.

Comme 80 % des études donnent un R0 entre 1,62 et 4,71, il faudrait qu’au moins 38 % à 78 % de la population générale soit immunisée – soit par infection, soit naturellement, soit par un vaccin – pour que nous puissions être raisonnablement sûrs que l’épidémie touche à sa fin. Si nous considérons la moyenne (non-pondérée) de toutes ces études, 3,14 en pratique, il faudrait que 68 % de la population soit immune avant que le désastre Covid-19 prenne vraiment fin.

La question n’est pas neutre. Dans le cas du SARS-CoV-2, un R0 de 5 au lieu de 2 nécessiterait des milliards de doses supplémentaires de vaccin dans le monde. Pire, si R0 est élevé, il suffirait d’un pourcentage suffisant de personnes refusant le vaccin pour que la maladie ne disparaisse pas. Et si l’immunité collective n’est obtenue que par l’infection, des millions de décès dans le monde se produiraient avant la fin de la pandémie.

Tous ceux qui pensent que c’est terminé prétendent implicitement que le R0 est très faible.

Mais est-ce vrai ?

Texte publié initialement sur Contrepoints

This post is also available in: EN (EN)